Practice Problems
Below are several problems for you to try on your own. We have worked out two problems for you, and the third is for you to try on your own. The answers are available on the Answer Key page, and you may get help from the sites listed on our Other Resources page.
Easy Problems
1. Find the reference angle of 300°.
Step 1: Determine which quadrant the terminal side of the angle can be found in.
In this case, the terminal side falls in Quadrant 4.
Step 2: Decide which formula should be used for the problem.
For a reference angle in degrees located in Quadrant 4, use the formula θ’ = 360°-θ.
Step 3: Plug angle into formula.
θ’ = 360°-300°
Step 4: Simplify to find reference angle.
θ’ = 60°
Evaluate the sine, cosine, and tangent of the angle (NO CALCULATOR!)
2. 225 °
Step 1: Determine whether the angle can be found on the unit circle, or whether you will have to use the reference angle.
In this case, the angle is part of the unit circle.
Step 2: Look on the unit circle to find the sine and cosine values.
Cosine= -√2/2, Sine= -√2/2
Step 3: Multiply sine by the reciprocal of cosine to find tangent.
-√2/2 x -2/√2= 1
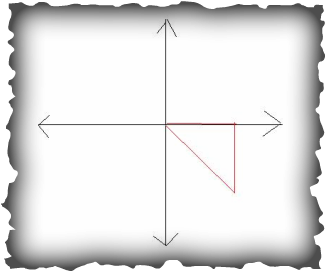
3. -150°
Practice Problem for you to try! Same instructions as question 2.
Step 1: Determine which quadrant the terminal side of the angle can be found in.
In this case, the terminal side falls in Quadrant 4.
Step 2: Decide which formula should be used for the problem.
For a reference angle in degrees located in Quadrant 4, use the formula θ’ = 360°-θ.
Step 3: Plug angle into formula.
θ’ = 360°-300°
Step 4: Simplify to find reference angle.
θ’ = 60°
Evaluate the sine, cosine, and tangent of the angle (NO CALCULATOR!)
2. 225 °
Step 1: Determine whether the angle can be found on the unit circle, or whether you will have to use the reference angle.
In this case, the angle is part of the unit circle.
Step 2: Look on the unit circle to find the sine and cosine values.
Cosine= -√2/2, Sine= -√2/2
Step 3: Multiply sine by the reciprocal of cosine to find tangent.
-√2/2 x -2/√2= 1
3. -150°
Practice Problem for you to try! Same instructions as question 2.
Medium Problems
Determine the values of the six trig functions of the angle at this point.
1. (7, 24)
Step 1: Write out the numbers as x and y.
x=7, y=24
Step 2: Use the pythagorean theorem to find the length of the hypotenuse.
a²+b²= c²
7²+24²= c²
49+576= c²
625= c²
√625=c
c=25
Step 3: Using the sides of x, y, and r (c is the same as r), write cosine, sine, and tangent.
sine= 24/25, cosine= 7/25, tangent= 24/7
Step 4: Flip the cosine, sine, and tangent values to get secant, cosecant, and cotangent
csc= 25/24, sec=25/7, cot= 7/24
Evaluate the sine, cosine, and tangent of the angle.
2. -25π/4
Step 1: Because the angle is negative, we must add π until it can be found on the unit circle.
-25π/4 + π = -25π/4 + 4π/4 = -21π/4 + 4π/4 = -17π/4 + 4π/4 = -13π/4 + 4π/4 = -9π/4 + 4π/4 = -5π/4
Step 2: Work clockwise around the unit circle until you find what positive angle the negative angle overlaps with.
In this case, the angle is in the same position as 3π/4.
Step 3: Use the sine, cosine, and tangent values of the positive angle for the negative angle, as they are the same.
sine= √2/2, cosine= -√2/2, and tangent= -1
Find the reference angle of the given value.
3. 2π/3
Practice problem for you to try!
1. (7, 24)
Step 1: Write out the numbers as x and y.
x=7, y=24
Step 2: Use the pythagorean theorem to find the length of the hypotenuse.
a²+b²= c²
7²+24²= c²
49+576= c²
625= c²
√625=c
c=25
Step 3: Using the sides of x, y, and r (c is the same as r), write cosine, sine, and tangent.
sine= 24/25, cosine= 7/25, tangent= 24/7
Step 4: Flip the cosine, sine, and tangent values to get secant, cosecant, and cotangent
csc= 25/24, sec=25/7, cot= 7/24
Evaluate the sine, cosine, and tangent of the angle.
2. -25π/4
Step 1: Because the angle is negative, we must add π until it can be found on the unit circle.
-25π/4 + π = -25π/4 + 4π/4 = -21π/4 + 4π/4 = -17π/4 + 4π/4 = -13π/4 + 4π/4 = -9π/4 + 4π/4 = -5π/4
Step 2: Work clockwise around the unit circle until you find what positive angle the negative angle overlaps with.
In this case, the angle is in the same position as 3π/4.
Step 3: Use the sine, cosine, and tangent values of the positive angle for the negative angle, as they are the same.
sine= √2/2, cosine= -√2/2, and tangent= -1
Find the reference angle of the given value.
3. 2π/3
Practice problem for you to try!
Challenging Problems
Find the six trig functions of the given angle. Watch for the domain constraints.
1. tan θ = -15/8 Constraints: sin θ < 0
Step 1: Looking at the sign on the trig function and the constraint, find the quadrant in which the angle lies.
Tangent is negative in this problem, and on the unit circle tangent is negative in quadrants 2 and 4. Sine is less than zero, which occurs in quadrants 3 and 4. Therefore, the angle must fall in quadrant 4 because both the angle and the constraint are negative in that quadrant.
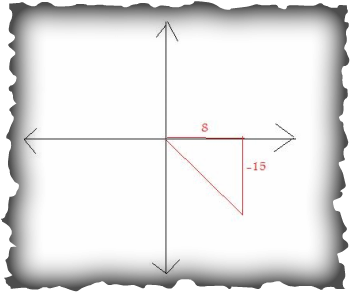
Step 2: Draw a triangle in Quadrant 4.
Step 3: Label the triangle using the information you are given.
In this case, we are given the value for tangent, which equals y/x. Therefore, we can label the side of the triangle on the x-axis "8" and the side parallel to the y-axis "-15".
In this case, we are given the value for tangent, which equals y/x. Therefore, we can label the side of the triangle on the x-axis "8" and the side parallel to the y-axis "-15".
Step 4: Use the pythagorean theorem to solve for the other side.
We are solving for r, and because r is always positive, we can leave the negative off the 15 in the equation.
a² + b² = c²
8² + 15² = c²
64 + 225 = c²
289 = c²
√289= c
c= 17
Step 5: Use the value of the sides to write all of the remaining trig functions.
sin= -15/17, cos= 8/17, csc= -17/15, sec= 17/8, cot= -8/15
Find the reference angle of the given angle.
2. -145°
Step 1: Find the positive equivalent of the negative angle.
To find the positive angle, subract 145 from 360.
360-145= 215°
Step 2: Determine what Quadrant the angle falls in.
In this case, 215° falls in quadrant 3.
Step 3: Use the corresponding equation to solve for the reference angle.
Because we are using the degree form of an angle in quadrant 3, we use the equation θ’= θ- 180°.
θ’= 215°-180°
θ’= 35°
Find the values of the six trig. functions for the given angle.
3. sec θ= -2 Constraint: sin θ > 0
Practice problem for you to try!
We are solving for r, and because r is always positive, we can leave the negative off the 15 in the equation.
a² + b² = c²
8² + 15² = c²
64 + 225 = c²
289 = c²
√289= c
c= 17
Step 5: Use the value of the sides to write all of the remaining trig functions.
sin= -15/17, cos= 8/17, csc= -17/15, sec= 17/8, cot= -8/15
Find the reference angle of the given angle.
2. -145°
Step 1: Find the positive equivalent of the negative angle.
To find the positive angle, subract 145 from 360.
360-145= 215°
Step 2: Determine what Quadrant the angle falls in.
In this case, 215° falls in quadrant 3.
Step 3: Use the corresponding equation to solve for the reference angle.
Because we are using the degree form of an angle in quadrant 3, we use the equation θ’= θ- 180°.
θ’= 215°-180°
θ’= 35°
Find the values of the six trig. functions for the given angle.
3. sec θ= -2 Constraint: sin θ > 0
Practice problem for you to try!
Real World Application Problems
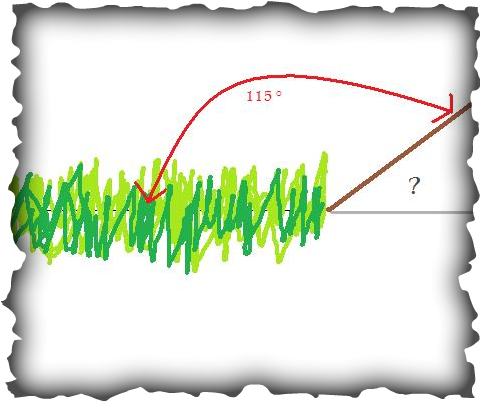
1. A wheelchair ramp has just been installed at a local care center. By law, the ramp must make a 45° or less with the ground. Does the new ramp (depicted below) comply with the requirement? Explain.
The angle in question is the reference angle of the given value. The angle that the ramp makes with the cement must be a 45˚ angle or less in order for it to be in regulation. To find the value of the angle, we use the given value of the terminal angle given. We take 115˚ and subtract it from 180˚ in order to find the angle in question.
180˚ - 115˚ = 55˚ So therefore the reference angle is 55˚ and the ramp is illegal!
180˚ - 115˚ = 55˚ So therefore the reference angle is 55˚ and the ramp is illegal!
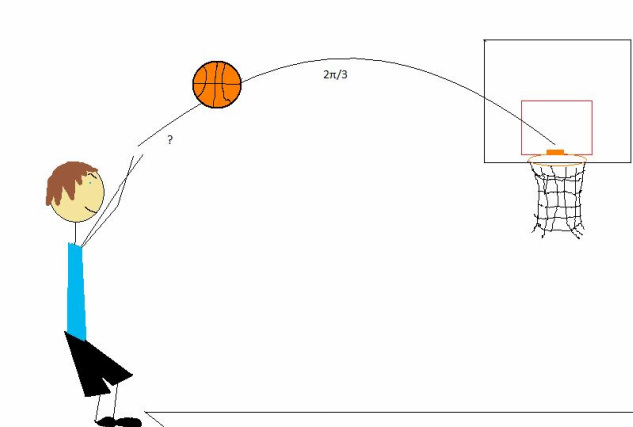
2. Willford is the best player on his basketball team. In order to win the basketball game, Willford must successfully shoot a freethrow. From his hands to the basket, a 180° arc must be formed. As he shoots the ball, Willford knows that the ball makes a 2π/3 arc with the basket. If we assume that Willford makes the basket, what angle does Willford's hands make with the basketball? (in degrees and radians)
In order to find the requested angle, we must use one of the reference angle formulas. Since the angle falls in Quadrant 2 on the unit circle, we can use the formula θ’= π-θ. When we plug in the angle, we get θ’= π-(2π/3), which is the same as θ’= (3π/3)-(2π/3). Once we subtract, we find that the arc from his hands to the ball is equal to π/3. To find the degree measure of the arc, we simply multiply π/3 by 180/π, which gives us 60° as the degree measure of the arc.
In order to find the requested angle, we must use one of the reference angle formulas. Since the angle falls in Quadrant 2 on the unit circle, we can use the formula θ’= π-θ. When we plug in the angle, we get θ’= π-(2π/3), which is the same as θ’= (3π/3)-(2π/3). Once we subtract, we find that the arc from his hands to the ball is equal to π/3. To find the degree measure of the arc, we simply multiply π/3 by 180/π, which gives us 60° as the degree measure of the arc.
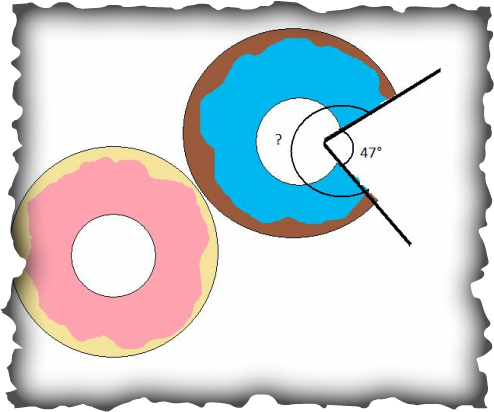
3. Bob bought two doughnuts at the student store. Each one forms a perfect 360° circle, but Bob has taken a bite out of one of them. Find the measure of the rest of the eaten doughnut in degrees and radians. Then find the total number of degrees and radians shared between both doughnuts.